Quops: a board game inspired by quantum mechanics


Quops (short for “quantum operations”) is a board game where the board and cards are based on the rules of quantum mechanics. The goal is simple: If you are player 0, get the values of all the tiles as close to 0 as possible. If you are player 1, get them as close to 1 as possible.
Each player has a hand of 5 cards, some of which affect a single tile and some of which affect two tiles. One-tile cards cannot be played on tiles entirely owned by your opponent, and two-tile cards must have one tile that is not completely owned by the opponent. On each turn, a player may use up to 3 cards, then draw back up to 5 at the end of their turn.
Tiles are hexagonal (six neighbors), and two-tile cards can only be played on neighboring tiles.
Mathematically, a board of n tiles is described by the superposition of bit vectors \([b_0, b_1, ... b_k]\) where \(k=2^n\). Player 0’s goal is to make the most probable state become \(\ket{00...0}\) while Player 1’s goal is to make it become \(\ket{11...1}\). This entire game could be described using quantum mechanics and matrices (and it is, in the code) - the only thing that the hexagonal board design decides is what possible unitary manipulations are allowed on the bits. In the backend, gameplay creates a quantum computer circuit step by step. In theory, this game could be physically implemented on a quantum computer, with each tile being a qubit.
Gameplay example
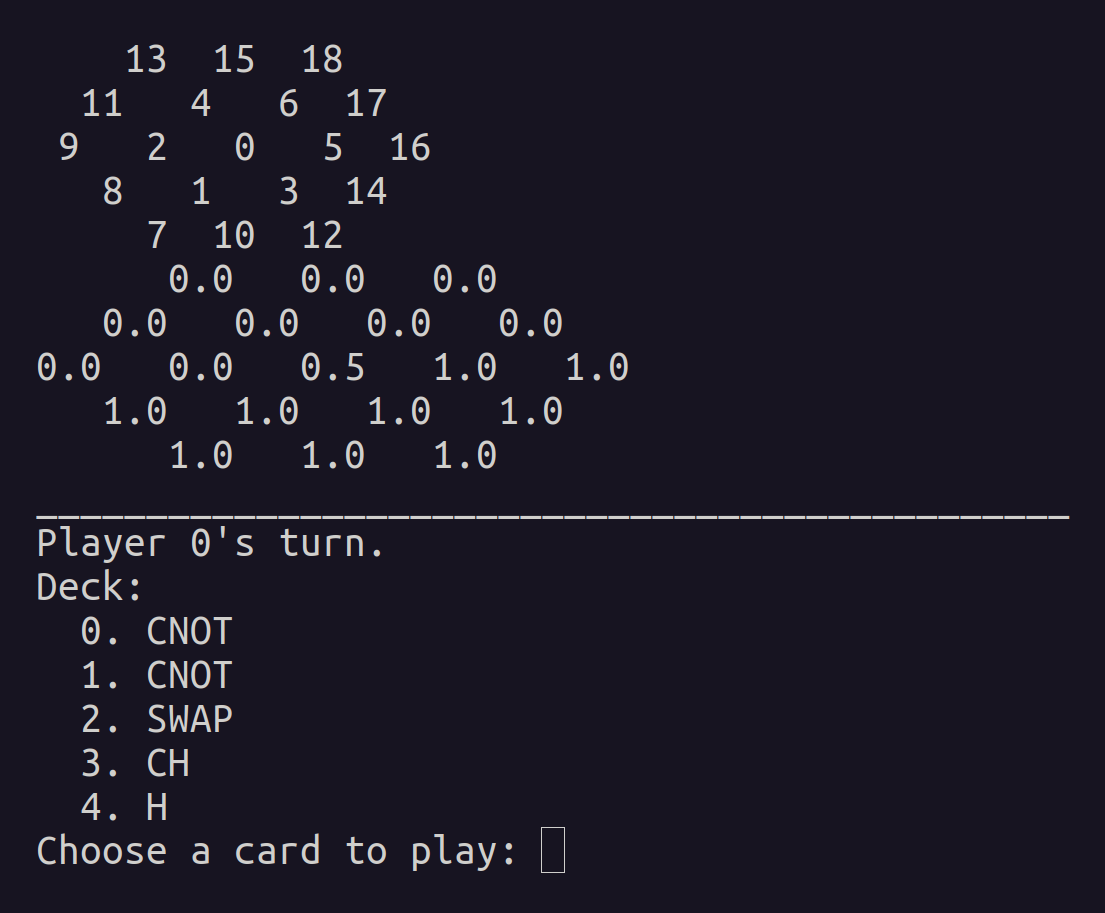
Tile numbering:
13 15 18
11 4 6 17
9 2 0 5 16
8 1 3 14
7 10 12
Gameplay:
GAME START
Board:
0.0 0.0 0.0
0.0 0.0 0.0 0.0
0.0 0.0 0.5 1.0 1.0
1.0 1.0 1.0 1.0
1.0 1.0 1.0
_______________________________________________
Player 0's turn.
Hand:
0. CNOT
1. X
2. CH
3. SWAP
4. H
Choose a card to play: 0
Target A: 6
Target B: 5
0.0 0.0 0.0
0.0 0.0 0.0 0.0
0.0 0.0 0.5 0.0 1.0 <-- tile 5 was flipped
1.0 1.0 1.0 1.0 because tile 6 is 1
1.0 1.0 1.0
_______________________________________________
...
...(Player 0 makes 2 more moves)
...
_______________________________________________
Player 1's turn.
Hand:
0. CH
1. SWAP
2. CH
3. CNOT
4. CNOT
Choose a card to play: 0
Target A: 8
Target B: 9
0.0 0.0 0.0
0.0 0.0 0.0 0.0
H gate --> 0.5 0.0 0.5 0.0 1.0
applied to 1.0 1.0 1.0 1.0
1.0 1.0 1.0
_______________________________________________
...
...Player 1 makes 2 more moves
...
_______________________________________________
Player 0's turn...
Qudits
What about more than 2 players (more than 2 possible states per tile)? In quantum computing, “qubits” with more than 2 states are known as qudits. \(n\) qudits that each have \(d\) states can represent \(d^n\) total possible “board-states” (ex: 2 qudits with 3 states each can represent the following 8 states: \(\ket{01}, \ket{02}, \ket{10}, \ket{11}, \ket{12}, \ket{20}, \ket{21}, \ket{22}\)). This game could be implemented using qutrits to allow for 3 players to play together, with each player aiming to get all qutrits into a different expected state.
TODO
- allow for operations to be inserted earlier in the program - i.e. have multiple “layers” of the board, and you can choose which layer to put an operation onto
- in-game tutorial/info on each of the cards
- in-game explanation of the basics of QC - make it accessible!
- work on game balancing (game currently works, but isn’t very fun)
- make an android/iOS/web app in unity!
- singleplayer puzzle campaign (slowly introduce different gates)
- online multiplayer??
- AI offline opponent
- different board types corresponding to different quantum architectures (different connectivities and native gates)
- transmon: nearest-neighbor, CNOT
- neutral atom: interaction radius, CZ, can’t place a gate within a certain radius of the previously-placed gate (if on the same layer)
- trapped ion: all-to-all, MS gate (maybe this is too complex?)
← back to jason-chadwick.com