Dancing the Quantum Waltz: Compiling Three-Qubit Gates on Four Level Architectures
International Symposium on Computer Architecture (ISCA 2023)


University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
University of Chicago
Abstract
Superconducting quantum devices are a leading technology for quantum computation, but they suffer from several challenges. Gate errors, coherence errors and a lack of connectivity all contribute to low fidelity results. In particular, connectivity restrictions enforce a gate set that requires three-qubit gates to be decomposed into one- or two-qubit gates. This substantially increases the number of two-qubit gates that need to be executed. However, many quantum devices have access to higher energy levels. We can expand the qubit abstraction of $\ket{0}$ and $\ket{1}$ to a ququart which has access to the $\ket{2}$ and $\ket{3}$ state, but with shorter coherence times. This allows for two qubits to be encoded in one ququart, enabling increased virtual connectivity between physical units from two adjacent qubits to four fully connected qubits. This connectivity scheme allows us to more efficiently execute three-qubit gates natively between two physical devices.
We present direct-to-pulse implementations of several three-qubit gates, synthesized via optimal control, for compilation of three-qubit gates onto a superconducting-based architecture with access to four-level devices with the first experimental demonstration of four-level ququart gates designed through optimal control. We demonstrate strategies that temporarily use higher level states to perform Toffoli gates and always use higher level states to improve fidelities for quantum circuits. We find that these methods improve expected fidelities with increases of 2x across circuit sizes using intermediate encoding, and increases of 3x for fully-encoded ququart compilation.
[.pdf] [publication] [arXiv]Selected Figures

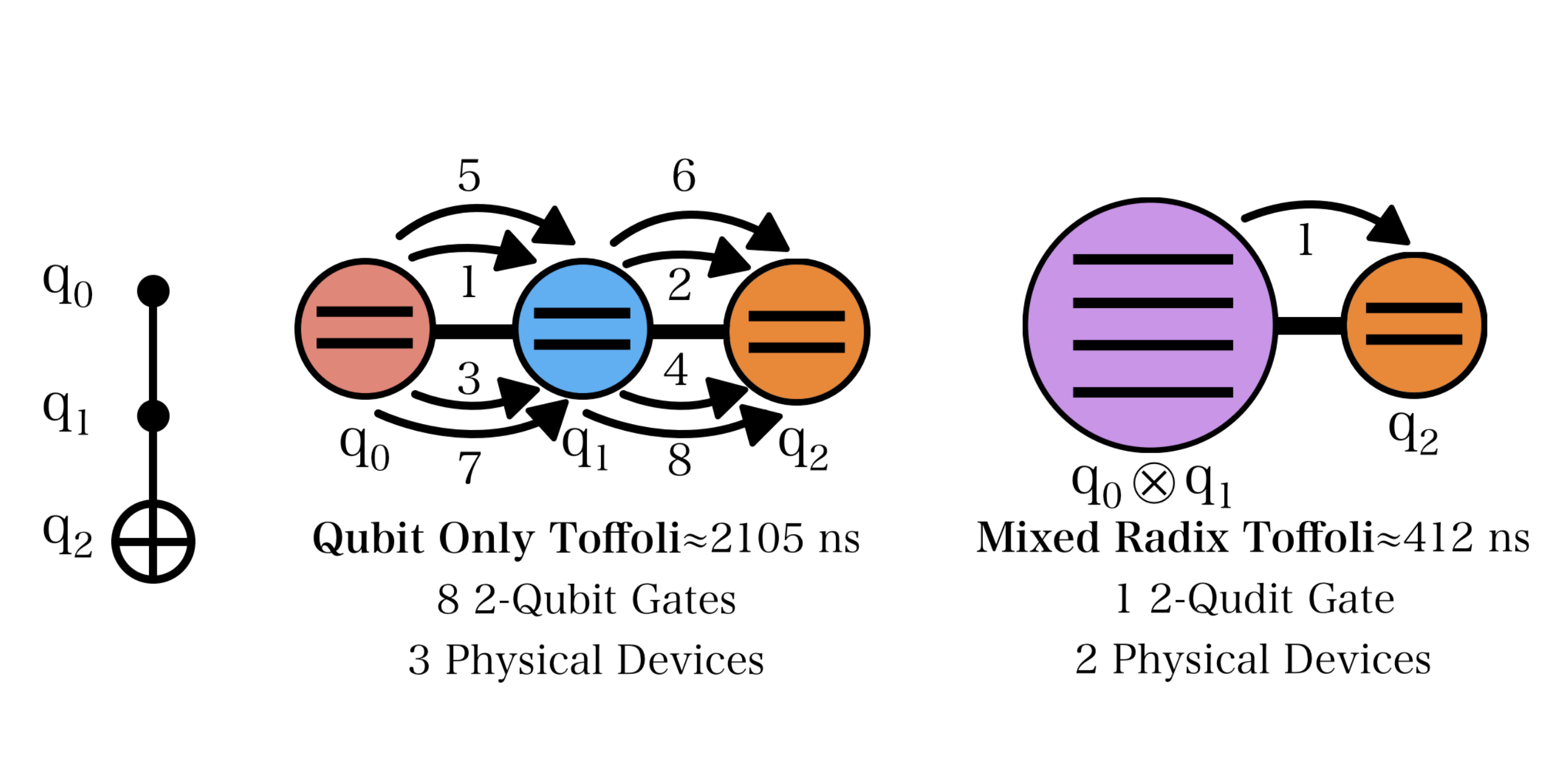
Figure 1. A comparison of a Toffoli gate execution on a three-qubit-only system versus a Toffoli gate execution on a ququart and qubit in a mixed-radix system. In a qubit-only system, we must use a decomposition that uses eight two-qubit gates that can be reduced to one two-qudit gate that has a shorter duration.
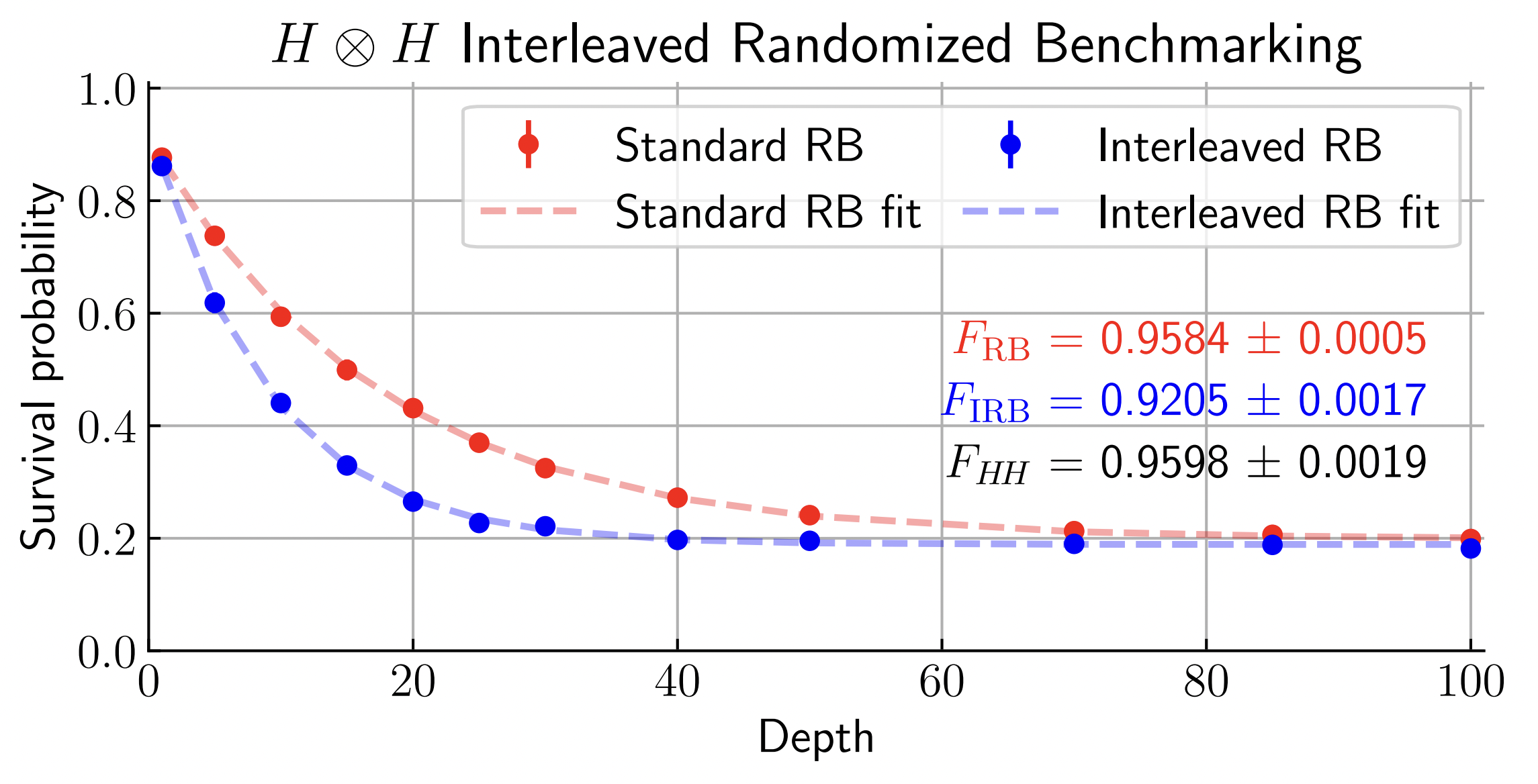
Figure 2. Interleaved Randomized Benchmarking for an optimal control $H \otimes H$ pulse on a superconducting transmon ququart following our qubit encoding. We use two-qubit Clifford sequences of gate depth up to 100 and average each data point over 10 samples. Error bars show the standard deviation of the mean but they are smaller than the mean markers. Red: Standard two-qubit Randomized Benchmarking to estimate the average Clifford gate fidelity to be $F_\mathrm{RB} \approx 95.8\%$. Blue: Interleaving the $H \otimes H$ pulse between the RB Cliffords yields a combined per-operation fidelity of $F_\mathrm{IRB} \approx 92.1\%$, resulting in an $H \otimes H$ fidelity $F_{H H} \approx 96.0\%$.
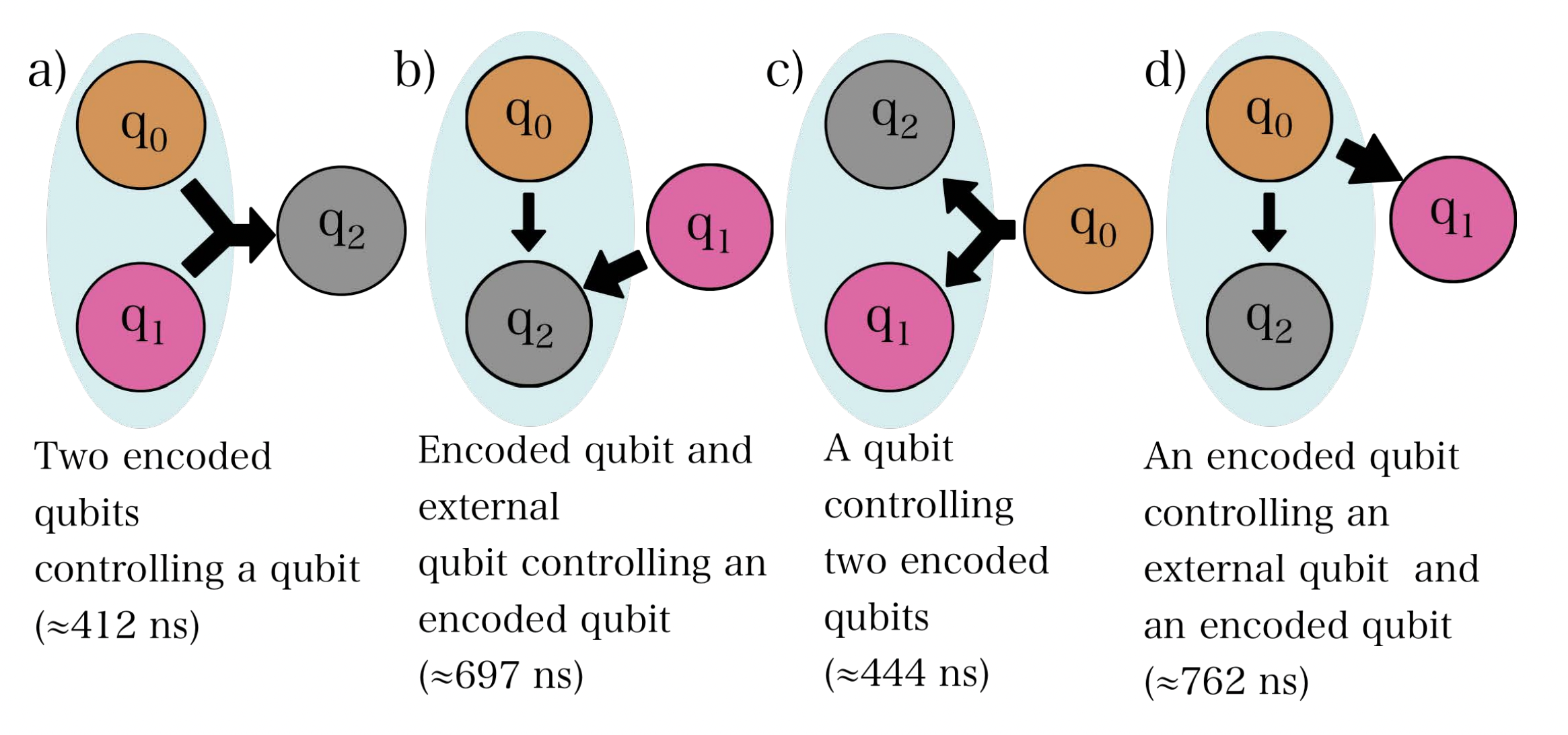
Figure 5. Examples of mixed-radix two-control and two-target gates. a) A configuration where both controls are encoded in the ququart and the target is mapped to a qubit. b) A configuration where the controls are split across the qubit and the ququart and the target is encoded in the ququart. c) A configuration where both targets are encoded in the ququart and the control is mapped to the qubit. d) A configuration where the targets are split across the qubit and the ququart and the control is encoded in the ququart.
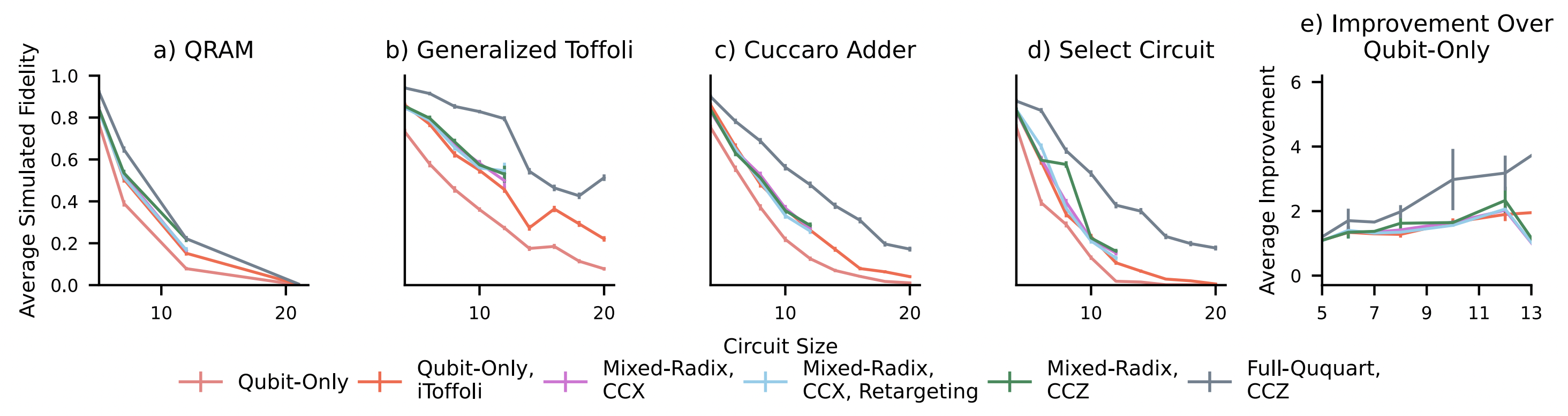
Figure 7. Simulated results for QRAM, Generalized Toffoli, Cuccaro Adder and Select Circuit from 5 to 21 qubits with different mixed-radix and full-ququart compilation strategies. The mixed-radix strategies do not have complete error bars due to the requirement to simulate a four-level system for every qubit which would require more than 86 GB of memory per circuit in our simulation framework. The final graph is the average fidelity improvement for each compilation method over the qubit-only compilation method as the size of the circuit increases.
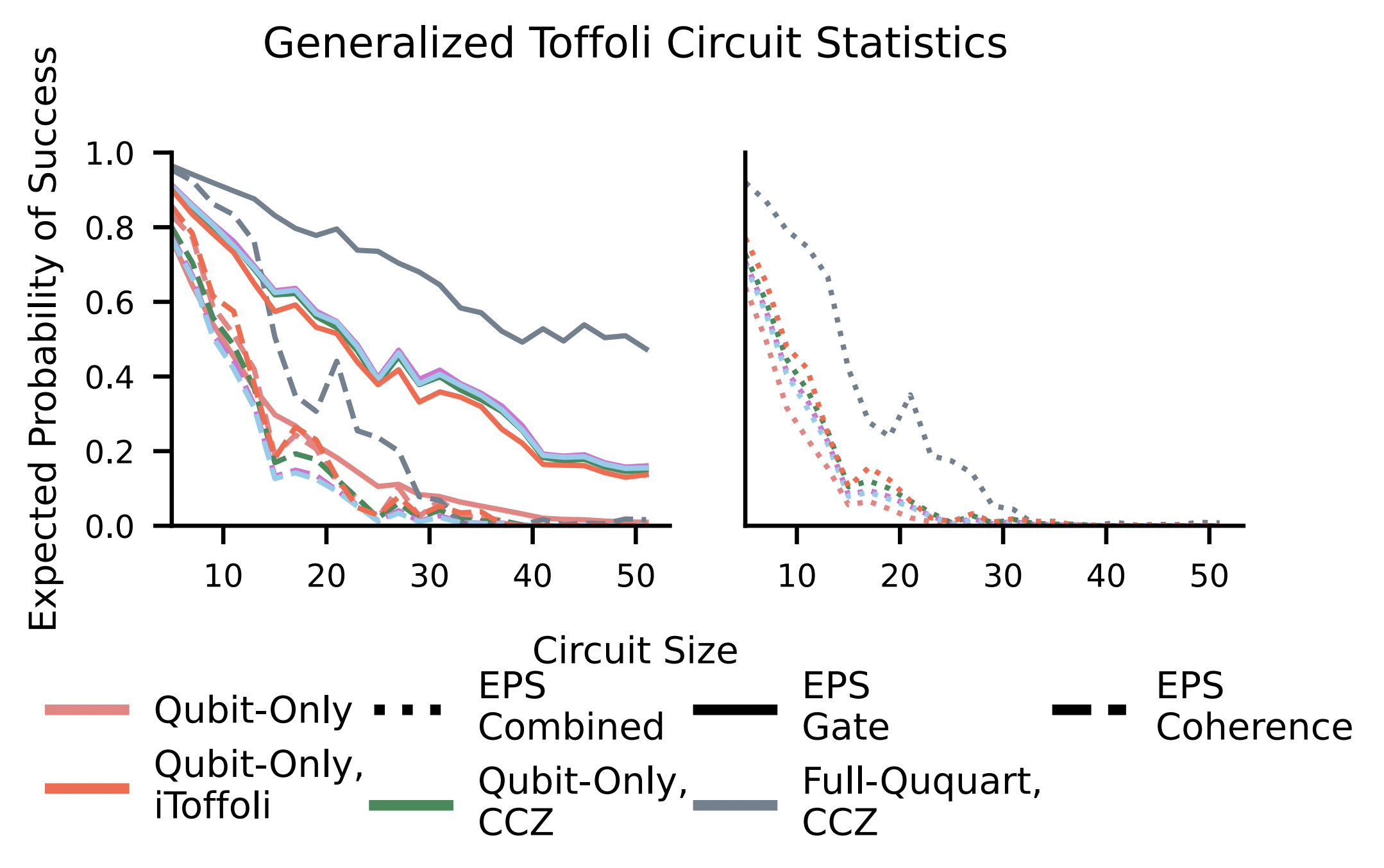
Figure 8. EPS statistics for the generalized Toffoli circuit. We show the gate and coherence EPS on the left and the product EPS on the right.
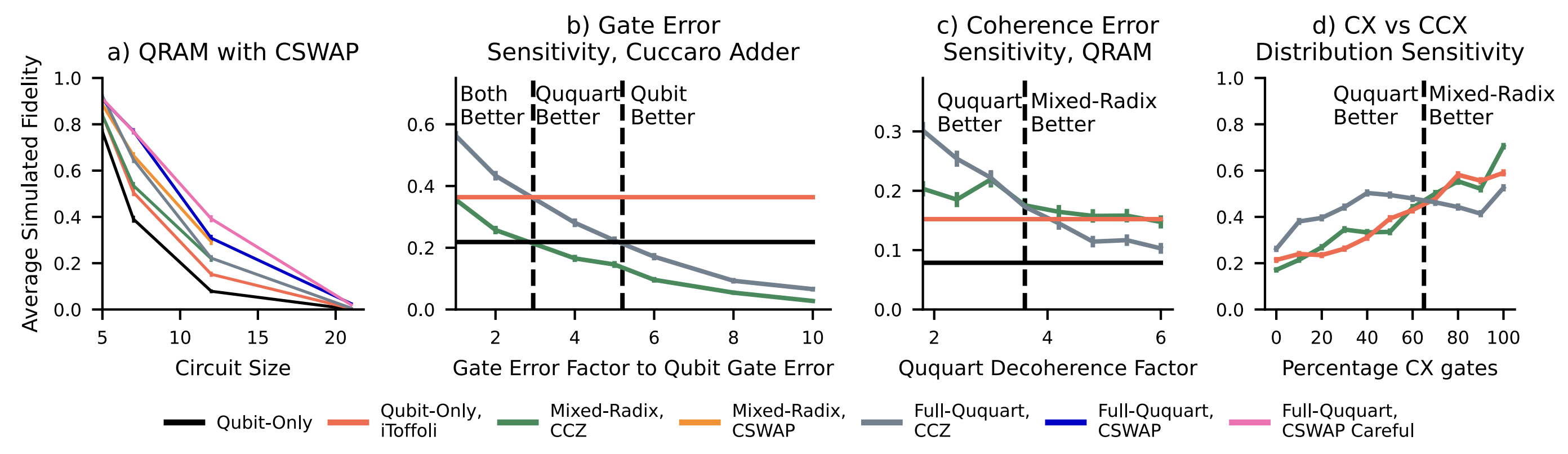
Figure 9. The results of several sensitivity studies. a) Sensitivity in simulation by using CSWAP gates in different orientations instead of decomposing to Toffoli gates. b) Changes in CCZ compilation strategies’ fidelities as gate error ququarts increases. c) Changes in CCZ compilation strategies’ fidelities as coherence error for the $\ket{2}$ and $\ket{3}$ level states changes. d) Differences in fidelities between mixed-radix and full-ququart compilation strategies as the distribution of CX gates to CCX gates in a circuit changes. In all graphs The black line represents the qubit-only fully-decomposed compilation method. The red line represents the qubit-only iToffoli-based decomposition. Below those points mixed-radix or full-ququart methods are more error prone than using only qubits. Please note the different scaling on the y-axis.
My Contributions
← back to jason-chadwick.com