Time-Efficient Qudit Gates through Incremental Pulse Re-seeding
IEEE International Conference on Quantum Computing and Engineering (QCE 2022)


University of Chicago
Carnegie Mellon University
University of Chicago
University of Chicago
University of Chicago
University of Chicago
Carnegie Mellon University
University of Chicago
University of Chicago
University of Chicago
University of Chicago
Carnegie Mellon University
University of Chicago
University of Chicago
University of Chicago
Abstract
Current efforts to build quantum computers focus mainly on the two-state qubit, which often involves suppressing readily-available higher states. In this work, we break this abstraction and synthesize short-duration control pulses for gates on generalized d-state qudits. We present Incremental Pulse Re-seeding, a practical scheme to guide optimal control software to the lowest-duration pulse by iteratively seeding the optimizer with previous results. We find a near-linear relationship between Hilbert space dimension and gate duration through explicit pulse optimization for one- and two-qudit gates on transmons. Our results suggest that qudit operations are much more efficient than previously expected in the practical regime of interest and have the potential to significantly increase the computational power of current hardware.
* indicates equal contribution
[.pdf] [publication] [arXiv] [poster]Selected Figures
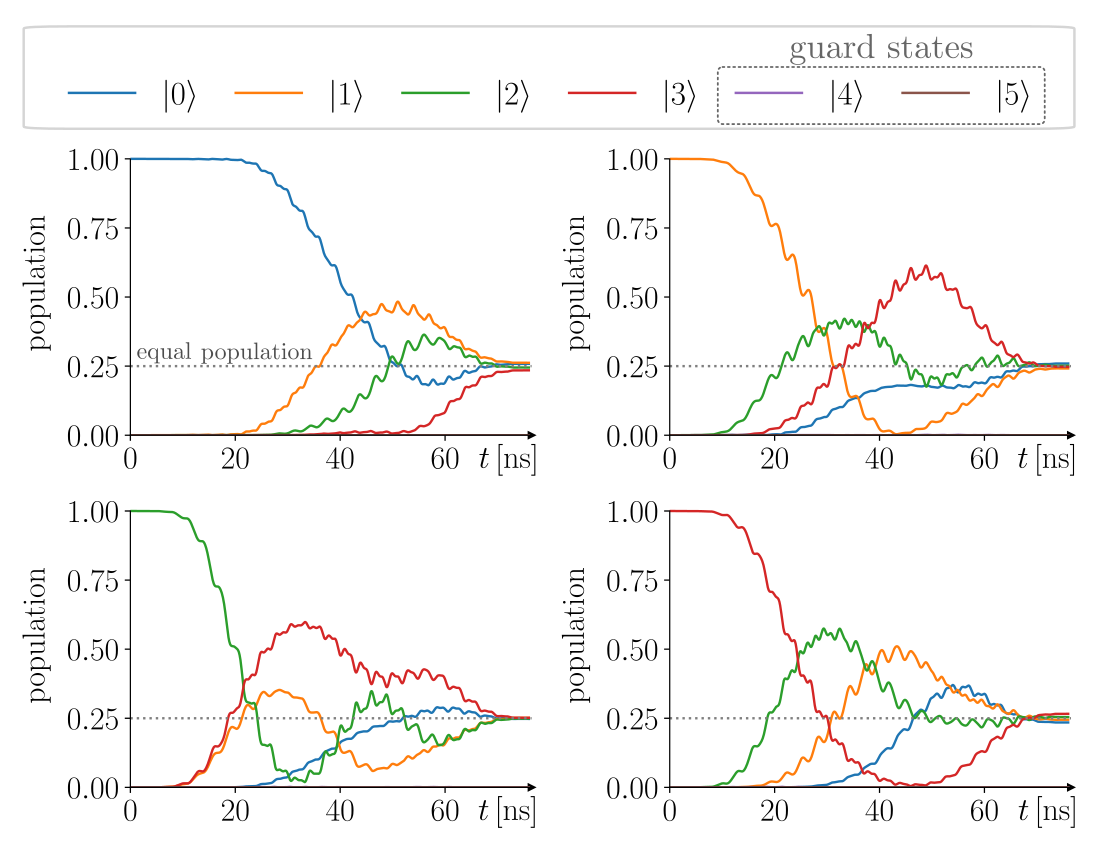
Figure 5. Evolution of state populations when applying the \(H_4\) pulse of shortest duration (\(76\,\mathrm{ns}\)) to a qudit with \(d=4\). Every computational basis state is transformed into superposition of all four basis states with nearly equal population, deviations only arising from the remaining \(0.1\%\) infidelity. At all times the populations of the guard states \(\ket{4}\) and \(\ket{5}\) are below \(2 \times 10^{-3}\) and \(10^{-6}\), respectively.
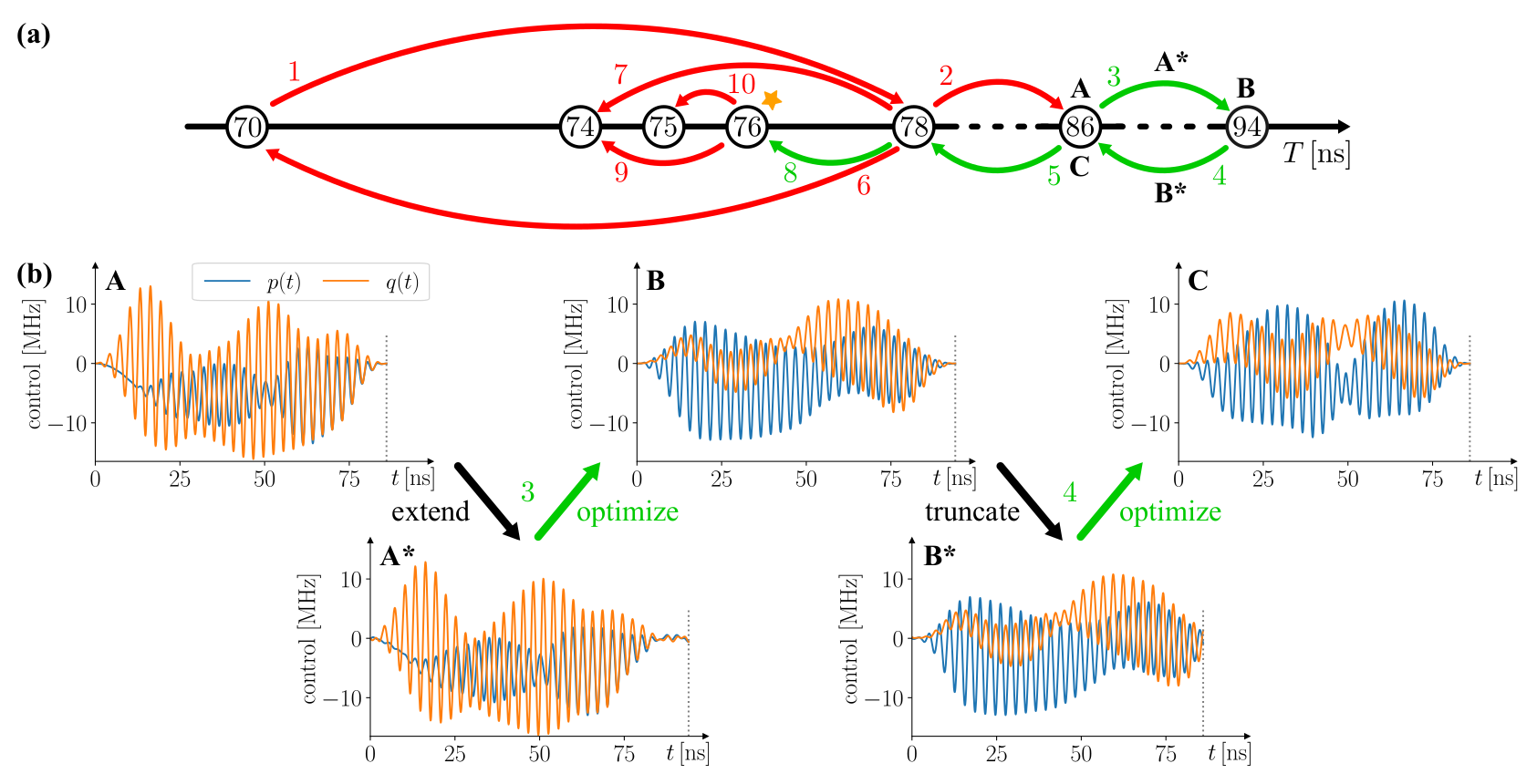
Figure 4. Applying Incremental Pulse Re-seeding (IPR) to find the shortest duration for the \(H_4\) gate. (a) Visualization of attempted durations during the IPR procedure, with the chronological order of steps indicated by the colored numbers. Green (red) arrows represent steps that did (did not) lead to meeting the pulse target fidelity of \(99.9\%\). Starting from \(T_\mathrm{start} = 70\,\mathrm{ns}\) and a time step of 8\,ns, three pulse extension and re-optimization steps are required before the target fidelity is first reached at \(94\,\mathrm{ns}\). The duration is then reduced to \(78\,\mathrm{ns}\) by successfully re-seeding with truncated pulses. After step \(6\) the time step is halved because re-optimizing at \(T=70\,\mathrm{ns}\) with the truncated pulse does not meet the target fidelity. Repeating this scheme leads to the final duration of \(T_\mathrm{gate} = 76\,\mathrm{ns}\), highlighted by the star, as after step \(10\) the time step falls below the granularity of \(1\,\mathrm{ns}\). (b) Plot A shows the optimized pulse after IPR step \(2\). A new seed for the optimization at \(T=94\,\mathrm{ns}\) is generated by extending the previous result in duration (A). At \(94\,\mathrm{ns}\) the target fidelity is met, so the optimized pulse is truncated (B) and used as a seed for the second \(T=84\,\mathrm{ns}\) optimization, leading to the successful result shown in C.
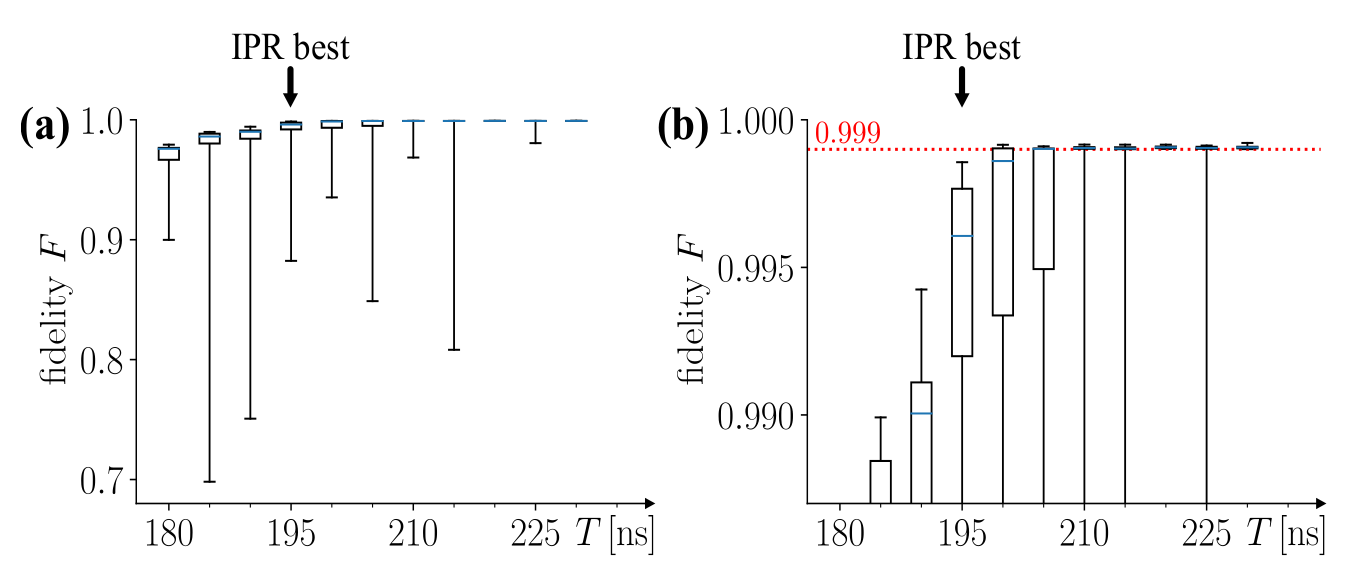
Figure 6. Distribution of naive random-guess optimizations of the \(X_8\) gate for invididual durations between \(180\,\mathrm{ns}\) and \(230\,\mathrm{ns}\). Each boxplot consists of \(20\) fidelities from \(20\) individual Juqbox optimizations, with the blue line indicating the median value, the box indicating the middle \(50\%\) of fidelities, and the whiskers indicating the full range of values. (a) The full data, showing a general increase in fidelity as duration increases. (b) Focusing on the area of interest (fidelities close to \(99.9\%\)). The IPR scheme outperforms random guessing, finding a minimum duration of \(T_\mathrm{best}=195\,\mathrm{ns}\) at \(99.9\%\) fidelity, whereas none of the 20 random guesses at that duration reached the same fidelity.

Figure 7. Dependence of single-qudit gate durations from qudit dimension \(d\) for four generalized single-qudit gates. Each data point shows the minimum duration of applying Incremental Pulse Re-seeding (IPR) from ten different starting times. The unexpected discrepancy between \(d=6\) and \(d=7\) for the generalized \(T_d\) gate suggests a highly complicated optimization space and shows that shorter pulses for some \(d\) values may be possible. For each gate the scaling of duration with dimension \(d\) is analyzed with quadratic and linear regressions, where the latter is less accurate but captures the essential behavior in this low-dimensional regime.
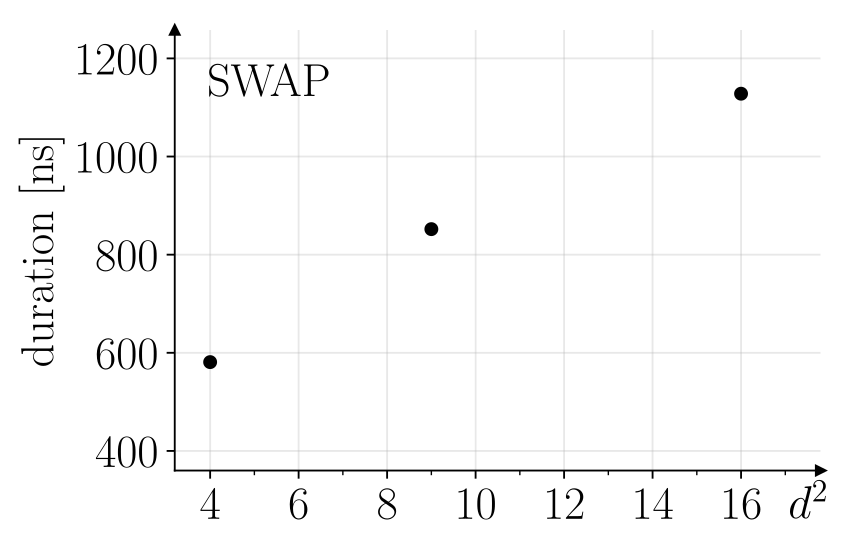
Figure 8. Gate durations of two-qudit \(\mathrm{SWAP}\) operations for qudit dimensions \(d=2, 3, 4\). The horizontal axis corresponds to the dimension of the full Hilbert space, \(h=d^2\). Due to the low number of data points, regression is not applied, but a near-linear trend is visible.
My Contributions
← back to jason-chadwick.com